Fonksiyon nedir, özellikleri, grafikleri, problemlerle ilişkisi ve kullanımı hakkında bilgi edinin.

Fonksiyonlar Nedir?

Fonksiyonlar Nedir? Matematikte, birçok farklı tanımı bulunan ve genellikle bir değişkeni başka bir değişkene bağlayan bir ilişki olarak tanımlanan fonksiyonlar, matematiksel problemlerin çözümünde ve grafiklerin çiziminde sıkça kullanılan bir kavramdır. Bir fonksiyon, her giriş değerine karşılık gelen bir çıkış değeri olan bir ilişki olarak da düşünülebilir. Bu ilişki genellikle bir formül veya kural yardımıyla ifade edilir.

Fonksiyonların temel özellikleri arasında tekil değerlilik, tanımlı olma ve bağıl tamlık gibi kavramlar bulunur. Bir fonksiyon, her giriş değeri için yalnızca bir çıkış değeri üretiyorsa bu fonksiyonun tekil değerlilik özelliğine sahip olduğu söylenir. Ayrıca, fonksiyonun tanım kümesinin tamamında bir değere karşılık gelmesi durumuna tanımlı olma, bağımsız değişkenin değerlerinin tüm doğal sayılardan oluştuğu duruma ise bağıl tamlık denir.

Fonksiyonlar, matematik problemlerinin çözümünde de sıkça kullanılır. Birçok matematiksel ilişki ve problem, fonksiyonlar yardımıyla modellenebilir ve çözülebilir. Özellikle AYT Matematik sınavlarında fonksiyonlar ve problemlerle ilişkilendirme soruları sıkça karşımıza çıkar. Bu nedenle, fonksiyonlar hakkında sağlam bir temel bilgiye sahip olmak, matematikte başarılı olmak için önemlidir.

Fonksiyonların Özellikleri

Fonksiyonların Özellikleri

Fonksiyonlar matematikte oldukça önemli kavramlardır. Bir fonksiyon, her bir x değeri için y değerini döndüren bir ilişki olarak tanımlanabilir. Fonksiyonların bazı önemli özellikleri vardır. İlk olarak, her x değeri için y değeri tek bir sonuç döndürür. Yani, aynı x değeri için farklı y sonuçları olamaz. Bu özellik fonksiyonların tekil olmasını sağlar. İkinci olarak, her x değeri için bir y değeri bulunabilir. Yani, herhangi bir x değeri için fonksiyonun tanım kümesinde bir karşılık bulunur. Bu özellik fonksiyonların tam olmasını sağlar. Üçüncü olarak, her fonksiyonun bir alanı ve kod alanı vardır. Alan, fonksiyonun girdi değerlerinin kümesini, kod alanı ise çıktı değerlerinin kümesini ifade eder.

İşte bu özellikler fonksiyonların temel karakteristikleridir ve matematik problemlerini çözerken bu özellikleri göz önünde bulundurmak önemlidir. Fonksiyonlar, matematik problemlerini çözmek için oldukça kullanışlı bir araçtır ve özelliklerine hakim olmak problemleri daha kolay çözmeyi sağlar.

Fonksiyonların Grafikleri

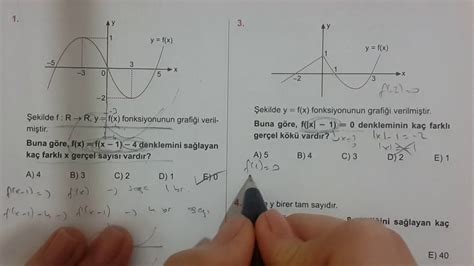
Fonksiyonların Grafikleri, matematikte fonksiyonların görsel temsilleridir. Bir fonksiyonun grafiği, x-y koordinat düzleminde, fonksiyonun çıktılarının gösterildiği bir grafiktir. Fonksiyonun bağımlı ve bağımsız değişkenlerinin ilişkisini anlamak ve görselleştirmek için grafikler kullanılır. Grafikler, fonksiyonların davranışlarını, tepe noktalarını, fonksiyonun artan veya azalan olduğu noktaları ve sıfırlarını göstermek için kullanışlıdır.

Fonksiyonların Grafikleri genellikle doğrusal veya eğrisel olabilir. Bir doğrusal fonksiyonun grafiği, bir çizgi şeklinde olup, denklemi genellikle y = mx + b şeklindedir. Diğer taraftan, eğrisel fonksiyonların grafikleri, daha karmaşık bir yapıya sahiptir ve farklı şekillerde olabilir. Örneğin, karekök fonksiyonunun grafiği parabol şeklindedir.

Matematikte Fonksiyonların Grafikleri ayrıca verilen bir fonksiyonun grafiği üzerinden fonksiyonun davranışını inceleme ve analiz etme imkanı sağlar. Grafikler, fonksiyonun belli aralıklarda artıp azaldığı noktaları, ekstremum noktalarını ve fonksiyonun sınırlarını belirlemek için kullanışlıdır. Bu nedenle, grafikler fonksiyonların görsel analizinde çok önemli bir rol oynar.

Problemlerle Fonksiyonları İlişkilendirme

Problemlerle Fonksiyonları İlişkilendirme
Problemlerle Fonksiyonları İlişkilendirme

Matematikte fonksiyonlar kavramı, problemlerle ilişkilendirilerek daha iyi anlaşılabilir. Fonksiyonlar, bir değişkenle diğer bir değişken arasındaki bağıntıyı ifade eder. Bu bağlamda problemlerle fonksiyonları ilişkilendirme, aslında matematik problemlerini gerçek hayatla ilişkilendirme becerisi kazandırır.

Fonksiyonlar sayesinde karşılaşılan problemleri matematiksel olarak çözebilir, değişkenler arasındaki ilişkiyi bulabilir ve bu ilişkiyi problem çözmede kullanabiliriz. Örneğin, bir sürekli fonksiyon yardımıyla bir nesnenin hareketini modelleyebiliriz. Bu sayede karşılaştığımız problemleri daha etkili bir şekilde çözebiliriz.

Problemlerle fonksiyonları ilişkilendirme, matematikte fonksiyon kavramının günlük hayatta nasıl kullanılabileceğini gösterir. Bu şekilde, öğrencilerin matematik kavramlarını daha iyi anlamasına ve problemleri çözmek için matematiksel düşünme yeteneklerinin gelişmesine yardımcı olur.

Fonksiyonların Problemlerde Kullanımı

Fonksiyonların Problemlerde Kullanımı

Fonksiyonların problemlerde kullanımı, matematikte çok önemli bir konudur. Problemlerle fonksiyonları ilişkilendirmek ve çözümlemek, matematik problemlerini çözmek için temel bir beceridir.

Bir fonksiyonun problemlerde kullanımı, genellikle verilen problemdeki bilinmeyen değerlerin belirlenmesi veya ilişkili olduğu diğer büyüklüklerle analiz edilmesi için kullanılır. Örneğin, bir problemdeki değişkenler arasındaki matematiksel ilişkiyi ifade etmek ve bu ilişkiyi çözerek problemdeki bilinmeyen değerleri bulmak için fonksiyonlar kullanılır.

Bazı problemlerde, bir fonksiyonun grafiği kullanılarak problemin görselleştirilmesi ve analiz edilmesi de gerekebilir. Fonksiyonların problemlerde kullanımı, matematiksel düşünme becerilerini geliştirmenin yanı sıra, gerçek hayattaki problemleri matematiksel olarak çözebilme yeteneğini de geliştirir.